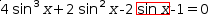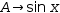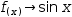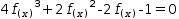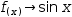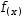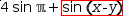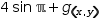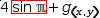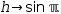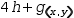3.5.2 Extract
Extract variable
and extract function transform the subject into
a variable or function reference and introduce a new definition into the
workspace whose elaboration is the subject.
In both cases, all subexpressions of the active expression that match the subject are
replaced by the reference.
The name of the new definition is
chosen to be different from any other name
in the workspace. If a new name cannot be chosen,
Myron prompts for a new name. The parameters of a new function are taken from the variables
in the subject. If the subject has no variables, extract function behaves like extract variable.
For example, given the source and subject
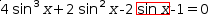 4⋅sin x^3+2⋅sin x^2-2⋅.{sin x}-1=0, apply Extract Variable from the Equations menu. If the name chosen is
A
the original expression becomes
4⋅sin x^3+2⋅sin x^2-2⋅.{sin x}-1=0, apply Extract Variable from the Equations menu. If the name chosen is
A
the original expression becomes
 4⋅A.^3+2⋅A.^2-2⋅A.-1=0
and the variable
4⋅A.^3+2⋅A.^2-2⋅A.-1=0
and the variable 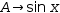 A.→sin x is introduced into the workspace.
A.→sin x is introduced into the workspace.
The same example with Extract Function introduces 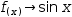 f(x)→sin x and changes the original expression to
f(x)→sin x and changes the original expression to
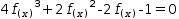 4⋅f(x)^3+2⋅f(x)^2-2⋅f(x)-1=0
4⋅f(x)^3+2⋅f(x)^2-2⋅f(x)-1=0
The original expression can be recovered using Substitute . Provided the introduced definition
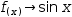 f(x)→sin x
remains in the workspace, substituting
f(x)→sin x
remains in the workspace, substituting
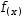 f(x)
in the original equation will offer
f(x)
in the original equation will offer
 sin x
as a substitution candidate.
sin x
as a substitution candidate.
The subject need not contain exactly one variable; it may contain none or more than one.
This is illustrated by the expression 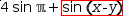 4⋅sin ℼ+.{sin (x-y)}.
With the subject shown, Extract Function introduces
4⋅sin ℼ+.{sin (x-y)}.
With the subject shown, Extract Function introduces  g(x, y)→sin (x-y) and changes the active expression
g(x, y)→sin (x-y) and changes the active expression
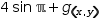 4⋅sin ℼ+g(x, y). With the selection
4⋅sin ℼ+g(x, y). With the selection 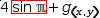 4⋅.{sin ℼ}+g(x, y), the subject contains no variables
and Extract Function operates like Extract Variable , introducing
4⋅.{sin ℼ}+g(x, y), the subject contains no variables
and Extract Function operates like Extract Variable , introducing
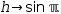 h→sin ℼ and changes the active expression to
h→sin ℼ and changes the active expression to 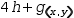 4⋅h+g(x, y).
4⋅h+g(x, y).
In some ways Extract is the inverse of Substitute. However, it is not
a complete inverse, since Substitute has other capabilities. Recall Substitute can
replace any subexpression, not just a reference. In contrast, Extract introduces
just a variable or function reference.